Question

Solve the polynomial equation by factoring and then using the zero product principal

Answer 1

Given: The polynomial below

`x^3+2x^2=9x+18`

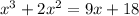
To Determine: The factored form of the equation using the zero product principle

Step 1: Put all the terms to the left hand side of the equation

`\begin{gathered} x^3+2x^2=9x+18 \\ x^3+2x^2-9x-18=0 \end{gathered}`

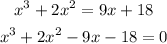
Step 2: Group the equation into and factorize

`\begin{gathered} (x^3+2x^2)-(9x-18)=0 \\ x^2(x+2)-9(x+2)=0 \\ (x+2)(x^2-9)=0 \end{gathered}`

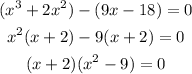
Step 3: Expand the difference of two squares

`\begin{gathered} a^2-b^2=(a-b)(a+b) \\ x^2-9^2=x^2-3^2=(x-3)(x+3) \end{gathered}`

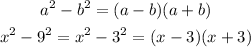
Step 4: Replace the difference of two squares with its equivalence

`\begin{gathered} x^3+2x^2=9x+18 \\ x^3+2x^2-9x-18=0 \\ (x+2)(x^2-9)=0 \\ (x+2)(x-3)(x+3)=0 \end{gathered}`

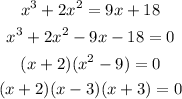
Step 5: Use the zero product principle to determine the solution set

`\begin{gathered} (x+2)(x-3)(x+3)=0 \\ x+2=0,or,x-3=0,or,x+3=0 \\ x=-2,or,x=3,or,x=-3 \end{gathered}`

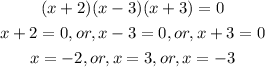
Hence,

The factored form is (x + 2)(x - 3)(x + 3) = 0

The solution set is x = -2, 3, -3