Given,
The expression is,
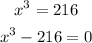
The rational theorem tells that if the polynomial has the rational 0 then it must be a fraction p/q, where p is a factor of constant term and q is the factor of leading coefficient.
The constant term 216 with factors:
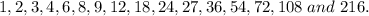
The leading coefficient is 1, with a single factor of 1.
![\begin{gathered} (p)/(q)=\frac{factor\text{ of 216}}{factor\text{ of 1}}=\pm(1)/(1),\operatorname{\pm}(2)/(1),\operatorname{\pm}(3)/(1),\operatorname{\pm}(4)/(1),\operatorname{\pm}(6)/(1),\operatorname{\pm}(8)/(1),\operatorname{\pm}(9)/(1),\operatorname{\pm}(12)/(1), \\ \operatorname{\pm}(18)/(1),\operatorname{\pm}(24)/(1),\operatorname{\pm}(27)/(1),\operatorname{\pm}(36)/(1),\operatorname{\pm}(54)/(1),\operatorname{\pm}(72)/(1),\operatorname{\pm}(108)/(1),\operatorname{\pm}(216)/(1) \end{gathered}]()
Substitute the possible roots one by one into the polynomial to find the actual roots. Start first with the whole numbers.
p(6)=0 so x=6 is a root of a polynomial p(x).
Using factor theorem to find the remaining roots,
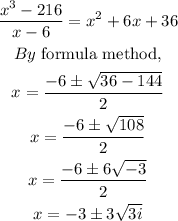
Hence, the roots are 6, -3-3sqrt(3)i, and -3+3sqrt(3)i. So, option A is correct.