Question

The product of two whole numbers is 592 and their sum is 53. What are the two numbers?

Answer 1

To solve this problem, we have to build two equations with the given information. Using x and y to represent the two numbers:

• Equation 1

`x* y=592`

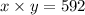
• Equation 2

`x+y=53`

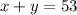
Now that we have to equations, we have to isolate one variable from one equation and replace it in the other.

`x=53-y`

Then, we will replace this value of x in Equation 1:

`(53-y)\cdot y=592`

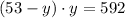
Solving for y we get:

`53y-y^2=592`
`-y^2+53y-592=0`

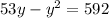
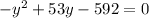
As we got this expression, we will have to use the General Quadratic Formula. With the help of a calculator, we get both values:

`y_1=16`
`y_2=37`

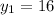
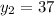
Finally, we have to replace these values in Equation 1 to evaluate which meets the condition:

`x_1=(592)/(y_1)`
`x_1=(592)/(16)=37`
`x_2=(592)/(y_2)`
`x_2=\frac{592}{37_{}}=16`

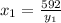
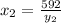
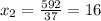
We have to evaluate the values in each equation:

`\begin{gathered} 37+16=53 \\ 53=53 \end{gathered}`
`37\cdot16=592`

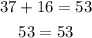
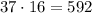
The first numbers meet the condition.

Answer: 37 and 16