The required solution is the circumference of the circle for the given radius or diameter
The formula for the circumference of a circle with radius r is :
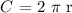
The formula for the circumference of a circle with diameter d is:
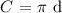
For the first circle with a radius of 12m:
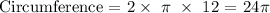
For the second circle with a diameter of 18in :
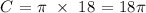
For the third circle with a radius of 2.8ft:
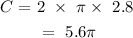
For the fourth circle with a diameter of 35km:
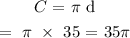
For the fifth circle with a radius of 7mm:
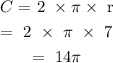
For the sixth circle with a radius of 15.6 cm:
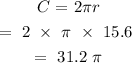
Note: Circumference has a unit. It's unit depends on the unit of the radius/ diameter