firstly you have to calculate the volume of the rectangular prism
volume = base area x height
since it is a rectangular prism
then the area = length x breath
length = 5cm , breath = 3cm
therefore
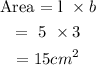
volume = base area x height
volume = 15 x 2
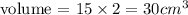
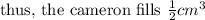
so the amount of the cameron fills that can fill up the prism is
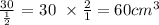
the answer is D