Question

Find the value of the investment at the end of 5 years

Answer 1

Given: Following details for an amount compounded annually-

`\begin{gathered} P=34900 \\ R=8\% \\ t=5\text{ years} \end{gathered}`

Required: To determine the amount after 5 years.

Explanation: The formula for compound interest is as follows-

`A=P(1+(r)/(n))^{(t)/(n)}`

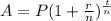
Here, A is the amount accrued.

P is the principal amount.

r is the annual rate as a decimal.

t is the time.

n is the number of times interest is compounded in a year.

In this case, the value of n=1 as we are calculating for annual compounding if the interest is compounded semiannually, n=2. For monthly, n=12. Finally, for daily n=365.

Now substituting the values in the formula as-

`\begin{gathered} A=34900(1+0.08)^5 \\ =34900(1.08)^5 \\ =\text{\$}51279.55 \end{gathered}`

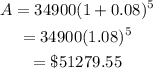
Final Answer: Investment after 5 years compounded annually is $51279.55