The scratching post is in the shape of a cylinder.
To cover the scratching post with a carpet, the surface of the post has to be covered.
This means that the amount of carpeting to be used will be equal to the total surface area of the pole.
The total surface area of the pole is calculated using the formula:
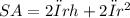
where r is the radius of the pole and h is the height of the pole.
The SECOND FORMULA is correct.