Question

You are designing a rectangda garden for the city park. The gardien is to have an area of 250 S feet, but you want to theamount of fending that you need to surround the garden. One length of the garden will not have a fence How many fees of lenong to you needto Surround the garden?

Answer 1

Consider the following picture

This is a sketch of the rectangular garden. We are given that the area of this rectangle is 200. Recall that the area of a rectangle is base * height. IN this case, we have the equation

`*\cdot\text{ y = 200}`

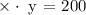
Now, note that we want to minimize the amount of fence we use. This means, that we want to minimize the perimIn this case we are told that we are not putting fence on one side of the rectangle. Since we want the less amount of fence to be used, and since y is the lenght of the longest side, we will assume that we are not fencing one of the y sides. So the perimeter of this rectangle is sum of the three remaining sides. Hence the function we want to minimize is

`y\text{ + 2x }`

From the first equation, we can replace the value of y with 200/x. So the function we want to minimize is

`(200)/(x)+2x`

Since we want to find the minimum of this function, we proceed by calculating its' derivative, make it equal to zero and the find the value of x that makes the equation true.

So, recall that the derivative of a term x^n is n x ^(n-1). In the case of 1/x, the value of n is n=-1. Also, recall that the derivative of a sum is the sum of the derivatives. So, applying this rule we get that the derivative of the function is

`200(-1)x^{^{\text{ -2}}}+2x^0=2\text{ - }(200)/(x^2)`

No, we will make it equal to 0 and find the value of x that makes the equation true. So we get the equation

`2\text{ - }(200)/(x^2)\text{ = 0 = }\frac{2x^2\text{ -200}}{x^2}`

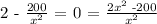
Since we have an equation of the form a/b =0 It must happen that a is 0. Then, we have the equation

`2x^2\text{ -200 =0}`

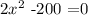
If we add 200 on both side, we get

`2x^2\text{ = 200}`

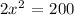
If we divide on both sides by 2, we get

`*^2\text{ = 100}`

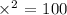
By taking the square root on both sides we get

`\text{ x = 10 or x = -10}`

Since x is a lenght, it should be positive. So we must have x = 10.

In this case, by replacing in the expression of y, we get that y = 200/10 = 20.

So we will need 2*10 + 20 = 40 feets long to surround the garden.