Given a radius and a central angle in radian, the formula in solving arc length is:
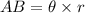
Since the angle and radius are given already in the problem, let's plug it in to the formula above.
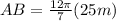
Then, solve.
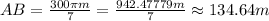
Therefore, the length of an arc having a central angle of 12π/7 is approximately 134.64 meters.