Question

the area of the shaded circular sector is equal to 30. The radius of the circle is 10. Find the measure of the central angle (in degrees)

Answer 1

Given:

There are given that the area of the shaded circular sector is:

`30\pi`

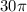
Step-by-step explanation:

To find the central angle, we need to use the formula of area of the sector:;

So,

From the formula of area of the sector:

`Area\text{ of sector=}\frac{central\text{ angle}}{360^(\circ)}*\pi r^2`

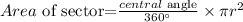
Then,

Put the value of area and radius into the above formula;

So,

`\begin{gathered} Area\text{ of sector=}\frac{central\text{ angle}}{360^{^(\circ)}}*\pi r^2 \\ 30\pi=(centralangle)/(360)\pi*(10)^2 \end{gathered}`

Then,

`\begin{gathered} 30\pi=(centralangle)/(360)\pi(10)^(2) \\ 3=(centralangle)/(36) \\ central\text{ angle=36}*3 \\ central\text{ angle=108}^(\circ) \end{gathered}`

Final answer:

hence, the central angle is 108 degrees.