Question

You randomly draw a marble, put it back, and then randomly draw a marble.What is the probability of drawing a yellow marble and then drawing a green marble? Write answer as a fraction.

Answer 1

Given:

The total number of marbles =7.

The number of yellow marbles = 2.

The number of green marbles =2.

The marbles are replaced after being drawn.

To find:

We need to find the probability of drawing a yellow marble and then drawing a green marble.

Step-by-step explanation:

The probability of drawing yellow marble P(Y).

`P(Y)=\frac{The\text{ number of yellow marbles}}{The\text{ total number of marbles}}`
`P(Y)=(2)/(7)`

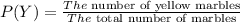
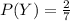
The probability of drawing green marble P(G).

`P(G)=\frac{The\text{ number of gr}een\text{ marbles}}{The\text{ total number of marbles}}`

`P(G)=(2)/(7)`

The probability of drawing a yellow marble and then drawing a green marble is

`=P(Y)* P(G)`

`=(2)/(7)*(2)/(7)`

`=(4)/(49)`

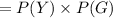
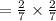
Final answer:

The probability of drawing a yellow marble and then drawing a green marble is 4/49.