The main point in this question, that the distance of the first part = the distance of the second part
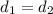
Since the speed of the first part is 6 mph
Let the time of it be t1
Since distance = speed x time, then
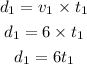
Since the speed of the second part is 3 mph
Let the time of it be t2, then
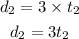
Equate d1 and d2 to find t2 in terms of t1
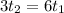
Divide both sides by 3
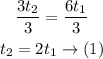
Since the total time of the two parts is 15 hours, then
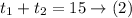
Substitute (1) in (2)
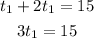
Divide both sides by 3
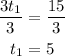
Now, let us find d1

Conner went 30 miles before his tire went flat