Consider the graph of f(x) = 5 ^ x + 1 1. Explain how to find the average rate of change between x = 0 and x = 4 . What is the average rate of change ?

Question

asked Jan 20, 2023 201k views

1 Answer

David Kristensen · Answer 1 · 2023-01-25T20:29:40+0000

1. To determine the average rate of change of a function "f(x)" between the points "x = a" and "x = b" we use the following formula:

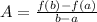
2. In this case, we have the following function:

And we have the points:

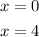
$\begin{gathered} x=0 \\ x=4 \end{gathered}$

Now we determine the value of f(b) by replacing x = 4 in the function:

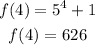
$\begin{gathered} f(4)=5^4+1 \\ f(4)=626 \end{gathered}$

Now we determine f(0):

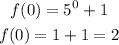
$\begin{gathered} f(0)=5^0+1 \\ f(0)=1+1=2 \end{gathered}$

Replacing in the formula for the average rate of change we get:

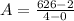
Solving the operations:

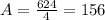
Therefore, the average rate of change is 156.