Question

Roseanna, Kennedy and Guadalupe had a super mean Math teacher who made them come up with a probability game where the chances of winning was 1/7. Roseanna’s idea was to have 5 red blocks and 30 blue blocks all in a bag. Each player gets one chance to pull out a block and if they pull out a red one they win Kennedy’s idea was the same as Roseanna’s except to have 1 red block and 7 blue blocks.Guadalupe’s idea was to have a seven sided die with a number 1 through 7 on each side. Each player rolls the die once and wins if they get a 3Whose game has a 1/7 chance of winning? Whose game doesn’t? For each game that doesn’t, show one way to change it so that it does have a 1/7 chance.

Answer 1

We are asked to determine which games have a 1/7 chance of winning. -

In the case of Roseanna's game, we have that there are 5 red blocks and 30 blues blocks. If the winner is the person that pulls out a red block then to determine the probability we must determine the quotient between the number of red blocks and the total number of blocks, like this:

`P(red)=(5)/(5+30)`

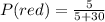
Solving the operations:

`P(red)=(5)/(35)=(1)/(7)`

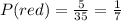
Therefore, Roseanna's game has a 1/7 probability.

In the case of Kennedy's game, there are 1 red block and 7 blue blocks, therefore, the probability of getting a red block is:

`P(red)=(1)/(7+1)=(1)/(8)`

Therefore, Kennedy's game has not a chance of 1/7 but 1/8 of winning.

For Kennedy's game to have a probability of 1/7 he could remove one of the blue blocks, that way the probability is:

`P(red)=(1)/(6+1)=(1)/(7)`

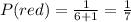
In the case of Guadalupe's game, we have that there is a dice with 7 sides numbered from 1 to 7. This means that the probability of getting a 3 is:

`P(3)=(1)/(7)`

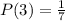
Therefore, Guadalupe's game has a probability of 1/7.