a) Consider the 7-digit registration code to be an arrangement of 7 cells to be filled using the given digits.
In the first cell, one can write any of the digits; on the other hand, there are only 6 digits available to fill the second cell (no number can be used more than once). Therefore, there are 5 digits that can be used in the third cell and so on; thus, there is a total of
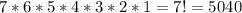
5040 different registration codes.
b) The 5040 different combinations found above are equally probable.
There are only 3 available even numbers (2, 4, and 6); therefore, we need to find the number of combinations such that none of the first three digits is equal to 2, 4, or, 6.
Thus, using a diagram,
There are 4 possible numbers that one can fit in the first cell (1,5,7, or 9), in the second cell, one can fit 3 numbers (any of the remaining ones from cell 1), and so on.
In the fourth cell (first cell in blue), one can fit any even number plus a remaining odd number from cell 3.
Therefore, the total number of codes such that their first three digits are not even are
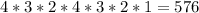
Then, the corresponding probability is
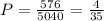
The answer to part b) is 4/35