Question

For a given geometric sequence, the common ratio, r, is equal to 5, and the 7th term, an, is equal to -43. Find the value of the 9thterm, a9. If applicable, write your answer as a fraction.a9=

Answer 1

Given:

it is given that common ration of a geometric sequence is r = 5 and 7th term is - 43.

Find:

we have to find the value of 9th term.

Step-by-step explanation:

we know the formula for nth term of a geometric sequence is

`a_n=ar^(n-1)`

since, 7the term is - 43,

Therefore, we have

`\begin{gathered} a_7=-43 \\ ar^(7-1)=-43 \\ ar^6=-43 \\ a(5)^6=-43 \\ a(15625)=-43 \\ a=-(43)/(15625) \end{gathered}`

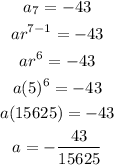
The 9the term of the geometric sequence is

`\begin{gathered} a_9=-(43)/(15625)*(5)^(9-1) \\ =-(43)/(15625)*(5)^8 \\ =-(43)/((5)^6)*(5)^8 \\ =-43*25 \\ a_9=-1075 \end{gathered}`

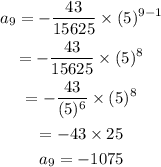
Therefore, 9th term of given geometric sequence is -1075.