The empirical rule is an approximation that can be used sometimes if we have data in a normal distribution. If we know the mean and standard deviation, we can use the rule to approximate the percentage of the data that is 1, 2, and 3 standard deviations from the mean. The rules is:
In this case, the mean is 44. The receptionist who answered less than 44 phone calls are to the left of the mean, and to the right are the ones who answered more. Since we want to know the percentage of phone calls numbering between 36 and 52, we know that:
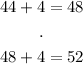
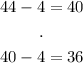
Thus, the lower bound is two standard deviations from the mean, and the upper bond is also 2 standard deviations from the mean.
Using the chart above, we can see that this corresponds to approximately 95% of the data.
The answer is approximately 95% of the data is numbering between 36 and 52