So we need to solve the following equation:
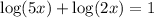
There are a few properties of logarithmic functions that we should remember. First, the logarithm of a negative number doesn't exist which means that x must be a positive number. Second, the addition of logarithms meets the following property:
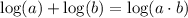
If we apply this to our equation we get:
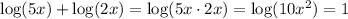
Now we can pass the logarithm to the right side of the equation:
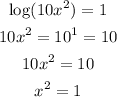
There are two possible solutions for x^2=1. These are x=1 and x=-1, however as I stated before x can't be a negative number which means that the solution of the equation is:
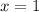
Then option C is the correct one.