1 Answer

Ieasha · Answer 1 · 2023-03-21T02:43:10+0000

Approximate Slope of a Function

We are given the function:

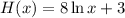
$H(x)=8\ln x+3$

We will find the approximate value of the slope at (e,11).

It's required to use 3 possible values of the approximation differential h.

Let's use h=0.1 and evaluate the function at x = e + 0.1 = 2.8182818

Compute:

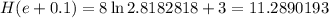
$H(e+0.1)=8\ln 2.8182818+3=11.2890193$

Compute the difference quotient:

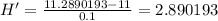
$H^(\prime)=(11.2890193-11)/(0.1)=2.890193$

Now we use h=0.01:

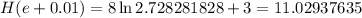
$H(e+0.01)=8\ln 2.728281828+3=11.02937635$

The difference quotient is:

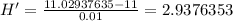
$H^(\prime)=(11.02937635-11)/(0.01)=2.9376353$

Finally, use h=0.001:

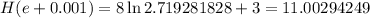
$H(e+0.001)=8\ln 2.719281828+3=11.00294249$
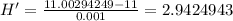
$H^(\prime)=(11.00294249-11)/(0.001)=2.9424943$

The last result is the most accurate, thus the slope of the tangent line is 2.94

Please log in or register to add a comment.