Solution
For this case we have the following data:
30, 40, 39, 36, 30
Representing the ages (in years) of the 5 doctors at a local clinic
these values represent an entire population, and we want to find the standard deviation of the population
1) First we need to calculate the mean
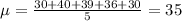
2) Now we can find the population variance like this:
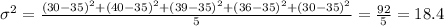
3) Calculate the population standard deviation
![\sigma=\sqrt[]{18.4}=4.29](https://img.qammunity.org/2023/formulas/mathematics/college/mihqwtvo091mpxvwtbqsqno7p8k68t9wma.png)
then the answer would be:
4.29