We have a segment AC, with the point B lying between A and C.
The ratio AB to BC is 5:6.
The coordinates for A and C are:
A=(2,-6)
C=(-4,2)
We can calculate the coordinates of B for each axis, using the ratio of 5:6.

We can do the same for the y-coordinates:
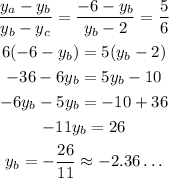
The coordinates of B are (-8/11, -26/11).