Question

Use the given conditions to find the exact values of sin(2u), cos(2u), and tan(2u) using the double-angle formulas.tan(u) = 13/5, 0 < u < /2

Answer 1

The first step to answer this question is to find tan(2u) by using the double angle formula:

`\begin{gathered} tan(2u)=(2tan(u))/(1-tan^2(u)) \\ tan(2u)=(2((13)/(5)))/(1-((13)/(5))^2) \\ tan(2u)=((26)/(5))/(1-(169)/(25)) \\ tan(2u)=((26)/(5))/(-(144)/(25)) \\ tan(2u)=-(65)/(72) \end{gathered}`

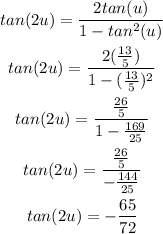
It means that tan(2u) is -65/72.

The next step is to rewrite the equations for sin(2u) and cos(2u) to have them in terms of the least number of variables possible, this way:

`\begin{gathered} sin(2u)=2sin(u)cos(u) \\ sin(2u)=2sin(u)(sin(u))/(tan(u)) \\ sin(2u)=(2sin^2(u))/(tan(u)) \end{gathered}`
`\begin{gathered} cos(2u)=cos{}^2(u)-sin^2(u) \\ cos(2u)=1-sin^2(u)-s\imaginaryI n^2(u) \\ cos(2u)=1-2sin^2(u) \end{gathered}`

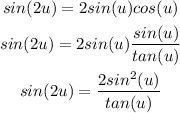
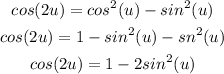
If we rewrite tan(2u) in terms of sin(2u) and cos(2u) we will have:

`\begin{gathered} tan(2u)=(sin(2u))/(cos(2u)) \\ tan(2u)=((2s\imaginaryI n^(2)(u))/(tan(u)))/(1-2sin^2(u)) \end{gathered}`

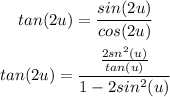
We know the values of tan(2u) and tan(u), so we can solve the equation for sin^2(u).

`\begin{gathered} tan(2u)=(2sin^2(u))/(tan(u)(1-2sin^2(u))) \\ -(65)/(72)=(2s\imaginaryI n^2(u))/((13)/(5)(1-2s\imaginaryI n^2(u))) \\ -(65)/(72)\cdot(13)/(5)\cdot(1-2sin^2(u))=2sin^2(u) \\ -(169)/(72)(1-2sin^2(u))=2sin^2(u) \\ -1+2sin^2(u)=(72)/(169)\cdot2sin^2(u) \\ -1+2sin^2(u)=(144)/(169)sin^2(u) \\ 2sin^2(u)-(144)/(169)sin^2(u)=1 \\ (194)/(169)sin^2(u)=1 \\ sin^2(u)=(169)/(194) \end{gathered}`

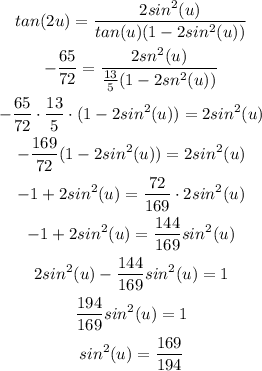
Using this value we can find the values of sin(2u) and cos(2u):

`\begin{gathered} sin(2u)=(2sin^2(u))/(tan(u)) \\ sin(2u)=(2\cdot(169)/(194))/((13)/(5)) \\ sin(2u)=(65)/(97) \end{gathered}`
`\begin{gathered} cos(2u)=1-2sin^2(u) \\ cos(2u)=1-2\cdot(169)/(194) \\ cos(2u)=1-(169)/(97) \\ cos(2u)=-(72)/(97) \end{gathered}`

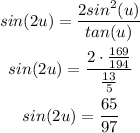
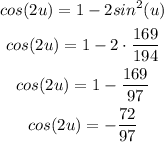
It means that sin(2u)=65/97, cos(2u)=-72/97 and tan(2u)=-65/72.