Question

Assume that random guesses are made for six multiple-choice questions on a test with five choices for each question so that there are n equals six trials each with the probability of success (correct) given by P equals 0.20. Find the probability of no correct answers.

Answer 1

Given in the question:

a.) Random guesses are made for six multiple-choice questions.

b.) There are five choices for each question.

c.) There are n equals six trials each with the probability of success (correct) given by P equals 0.20.

We will be using the Binomial Probability Formula:

`P(X=k)=(_nC_k)(p^k)(1-p)^(n-k)`

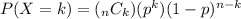
Where,

n = Number of trials = 6

P = Probability of success = 0.20

X = Correct answers

Let's evaluate the definition of binomial probability at k = 0 since we are tasked to find the probability of no correct answers.

`P(X=0)=(_6C_0)(0.20^0)(1-0.20)^(6-0)`
`P(X=0)\text{ = (}(6!)/(0!(6-0)!))(0.20^0)(0.80^6)^{}^{}`
`P(X=0)\text{ = }0.262144\text{ }\approx\text{ 0.26}2`

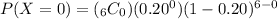
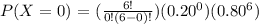
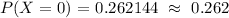
Therefore, the probability of no correct answers is 0.262 or 26.20%.