Question

Can someone help me with these geometry questions sorry it’s a two parter.

Answer 1

In this problem, we are trying to choose between using a permutation and a combination.

The main difference between the two is the order.

In a combination, order doesn't matter, but it does matter in a permutation. Since the coach is choosing people based on how they performed, this will be a permutation.

For the first box on your screen, you should drag and drop the "P" variable for permutation.

Next, we need to apply the permutation formula:

`_nP_r=(n!)/((n-r)!)`

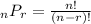
I'm assuming there are a total of 14 players on the team? So we will let

`\begin{gathered} n=14 \\ r=3 \end{gathered}`

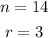
Where n represents the total number of players, and r represents the number of people being chosen based on performance. Then we have:

`(14!)/((14-3)!)=(14!)/(11!)`

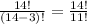
You can drag the 14! to the numerator and the 11! to the denominator.

Finally, we need to simplify to get the final answer. We can always use a calculator, but I'll show the steps for simplifying here:

`\begin{gathered} \text{ Rewrite}14! \\ (14\cdot13\cdot12\cdot11!)/(11!) \end{gathered}`
`\begin{gathered} \text{ Cancel the }11! \\ \\ \frac{14\cdot13\cdot12\cdot\cancel{11!}}{\cancel{11!}} \end{gathered}`

Multiply the remaining values:

`14\cdot13\cdot12=2184`

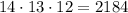
The coach has 2184 ways to choose a player.