Question

it doesn't matter which of the two points on a line you choose to call (x1,y1) and which you choose to call (x2,y2) to calculate the slope of the line . true or false.

Answer 1

True

Step-by-step explanation

the slope of a lines is the change in y over the change in x

`\text{slope}=\frac{change\text{ in y}}{\text{change in x}}=(y_2-y_1)/(x_2-x_1)`

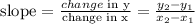
where

`\begin{gathered} \text{P1}=(x_1,y_1) \\ P2=(x_2,y_2) \end{gathered}`

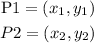
Step 1

Now, to prove , make

`\begin{gathered} P1(x_2,y_2) \\ P2(x_1,y_1) \\ \end{gathered}`

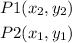
now, replace

`\begin{gathered} \text{slope}=(y_1-y_2)/(x_1-x_2) \\ \text{slope}=(y_1-y_2)/(x_1-x_2)=(-(y_2-y_1))/(-(x_2-x_1))=((y_2-y_1))/((x_2-x_1)) \end{gathered}`

and we get the same slope, it does not matter wich one of the two points we choose to call P1 and P2.

True

I hope this helps you