Let "A" represent the number of adults that ride the bus and "C" represents the number of children that ride the bus.
On a certain morning shift 1300 people rode the bus, this means that the number of adults and the number of children add up to 1300. You can express the total number of passengers on that shift as follows:
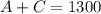
The child's fare is $0.50, so if C children ride the bus a total of 0.50C will be paid.
The adult's fee is $1.50, so if A adult rides the bus, the total earned will be 1.50A.
If you add both fares, you will determine the total fares for the shift, which was $1550
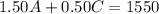
Using both equations you have determined the number of adults and children that rode the bus:
-First, write the first expression for one of the variables, for example, write it for A:
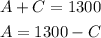
-Second, replace the expression obtained in the second equation
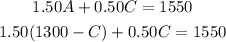
Now you have to solve for C
→ Distribute the multiplication on the parentheses term:
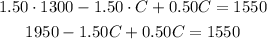
→Simplify the like terms
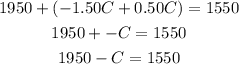
→Subtract 1950
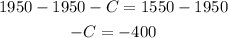
→ Multiply both sides by -1 to invert the sign:
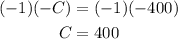
Finally, once you have determined the value of C, you can calculate the value of A as follows:
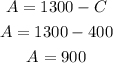
So, 400 children and 900 adults rode the bus.