Question

Which of the following represents vector vector t equals vector PQ in trigonometric form, where P (–13, 11) and Q (–18, 2)?

Answer 1

The coordinate of the vector P and Q are

`\begin{gathered} P(-13,\text{ 11)} \\ \text{And } \\ Q(-18,2) \end{gathered}`

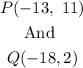
To find the vector PQ. we have

`\begin{gathered} t=\bar{PQ} \\ PQ\text{ is having the coordinate } \\ PQ=(-18-(-13),2-11)=(-5,-9) \end{gathered}`

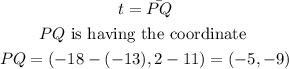
To find the vector, we use

`\begin{gathered} r=\sqrt[]{x^2+y^2} \\ \text{Where } \\ x=-5,y=-9 \\ r=\sqrt[]{(-5)^2+(-9)^2}=\sqrt[]{25+81}=\sqrt[]{106}=10.296 \end{gathered}`

Then we obtain the angle using

`\begin{gathered} \text{tan}\theta=((y)/(x))_{} \\ \text{Substituting the value of x and y, we have } \\ \tan \theta=((9)/(5))=\tan \theta=(1.8) \end{gathered}`

Hence

`\begin{gathered} \tan \theta=1.8 \\ \theta=\tan ^(-1)(1.8) \\ \theta=60.945 \end{gathered}`

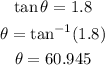
Hence

The vector in trigonometry form will be

`\begin{gathered} t=r(i\cos \theta+j\sin \theta) \\ \text{Then} \\ t=10.296\cos 60.945i+10.296\sin 60.945j \end{gathered}`

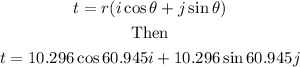
Therefore

t= 10.296 cos 60.945 i + 10.296 sin 60.945j

Answer: Option C(third option ).