In this question, we need to find the probability of pulling a red or brown candy from a bag.
We know that the bag contains the next amount of candies:
• 5 yellow candies
,
• 11 red candies
,
• 4 green candies
,
• 12 blue candies
,
• 7 brown candies
Therefore, in total, we have 39 candies.
Then the probability of pulling a red candy is:
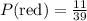
The probability of pulling a brown candy is:
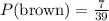
Now, we know that the general formula for the probability of two events is given by:
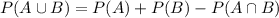
However, in this case, we do not have any probability that both events happen at the same time - in other words, they are mutually exclusive events. Therefore, we have:
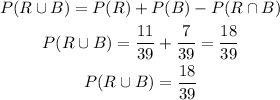
Therefore, in summary, the probability that a red or brown candy is pulled from the bag is 18/39 (option A.)