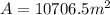Question

A training field is formed by joining a rectangle and two semicircles, as shown below. The rectangle is 98 m long and 70 m wide,Find the area of the training field. Use the value 3.14 for I, and do not round your answer. Be sure to include the correct unit in your answer.98 m

Answer 1

We are asked to determine the area of the given figure. The figure is composed of two semi-circles and a rectangle, therefore, the total area of the figure is:

`A=A_s+A_r+A_s`

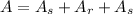
The area of the semicircle is given by:

`A_s=(1)/(8)\pi D^2`

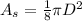
Where "D" is the diameter. Replacing the values we get:

`A_s=(1)/(8)(3.14)(70m)^2`

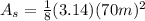
Solving the operations:

`A_s=1923.25m^2`

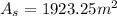
Now we determine the area of the rectangle using the following formula:

`A_r=wh`

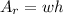
Where "w" and "h" are the dimensions of the rectangle. Replacing the values we get:

`\begin{gathered} A_r=(98m)(70m) \\ A_r=6860m^2 \end{gathered}`

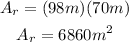
Now we replace the values in the formula for the total area:

`A=1923.25m^2+6860m^2+1923.25m^2`

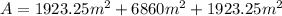
Solving the operations:

`A=10706.5m^2`