Question

6) What is the equation of the following graphed function?Is the vertex a maximum or minimum?What are the solutions to the function?What is the y-intercept?уmobruo uove56$ x

Answer 1

If we know the roots (solutions) we can find the equation of the second-degree function using the formula above:

`f(x)=a(x-x_1)(x-x_2)`

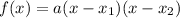
In this case, a = -1, x1 = 2 and x2 = 4. Therefore the equation will be:

`f(x)=-1(x-2_{})(x-4_{})`
`f(x)=-x^2+6x-8`

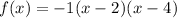
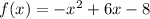
The vertex is maximum (see that the function has a clear max value).

The solutions to the function are the roots (place in the x-axis where the function cross). They are 2 and 4.

The y-intercept is the point with the format (0,y). Thus to find this point we can substitute 0 into the function:

`f(0)=-0^2+6*0-8`
`f(0)=-8`

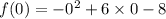
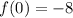
The y-intercept will be y = -8.