Question

Mr. Weinberg harvests apples from his apple tree each autumn. As the tree has matured since it's first crop, the weight in lbs, W, of the apple harvest has increased exponentially by 60% every 4 years according to the function W (t)=80(1.6)^ t/4, where the t is the number of years since the first crop.Based on this model, which is the best estimate for the percent change in the weight of the apple harvest from year to year?-26.5%-15.0%-40.0%-8.8%-12.5%

Answer 1

12.5%

Step-by-step explanation:

To know the percent of change from year to year, we will calculate the Weight for 2 consecutive years.

So, when t = 0, we get that W is equal to:

`\begin{gathered} W_0=80(1.6)^{\text{ t/4}} \\ W_0=80(1.6)^{\text{ 0/4}} \\ W_0=80 \end{gathered}`

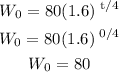
Then, when t = 1, we get:

`\begin{gathered} W_1=80(1.6)^{\text{ t/4}} \\ W_1=80(1.6)^{\text{ 1/4}} \\ W_1=89.97 \end{gathered}`

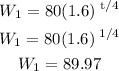
Now, we can calculate the percentage of change as:

`(W_1-W_0)/(W_0)*100=(89.97-80)/(80)*100=12.47\text{ \%}`

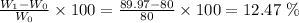
Therefore, the best estimate is 12.5%