Question

Line a is parallel to line b line a passes through the points (1,7) and (2,-4)Line b passes through the point (6,14)The equation of line b is y=__

Answer 1

Given:

Line a is parallel to line b.

Line a passes through the points (1,7) and (2,-4).

Line b passes through the point (6,14).

The objective is to find the equation of the line b in slope intercept form.

For parallel lines the slope of the two lines will be equal.

Consider the coordinates of the line a as,

`\begin{gathered} (x_1,y_1)=(1,7) \\ (x_2,y_2)=(2,-4) \end{gathered}`

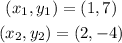
The slope of line a can be calculated as,

`\begin{gathered} m_a=(y_2-y_1)/(x_2-x_1) \\ =(-4-7)/(2-1) \\ =-11 \end{gathered}`

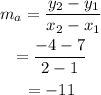
Since both are given as parallel lines, the slop of line b will be,

`m_b=-11`

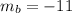
If the line b passes throught the point (6,14), the equation can be represented as,

`\begin{gathered} y-y_1=m(x-x_1) \\ y-14=-11(x-6) \\ y-14=-11x+66 \\ y=-11x+66+14 \\ y=-11x+80 \end{gathered}`

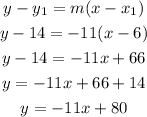
Hence, the equation of line b is y = -11x+80.