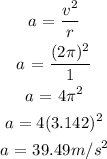Question

what is the centeipital force of a 0.2 kg ball traveling in a circle with a radius of 1 m if it completes one revolution every secondanswer is in meters per second squared

Answer 1

Answer:
`\begin{gathered} \text{Force, F = 7.9N} \\ \text{Acceleration, a = 39.49 m/s}^2 \end{gathered}`

Explanations:

The mass of the ball, m = 0.2 kg

Radius of the circle, r = 1 m

To convert the angular speed to rad per second from revolution per second, multiply by 2π

w = 1 rev/sec = 2π rad/sec

The velocity, v = wr

v = (2π) x 1

v = 2π m/s

The centripetal force is given by the formula:

`\begin{gathered} F\text{ = }(mv^2)/(r) \\ F\text{ = }(0.2*(2\pi)^2)/(1) \\ F\text{ = 0.2 }*\text{ 4}\pi^2 \\ F\text{ = 0.8}\pi^2 \\ F=0.8(3.142)^2 \\ F\text{ = 7.9 N} \end{gathered}`

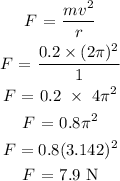
The centripetal acceleration is given as:

`\begin{gathered} a\text{ = }(v^2)/(r) \\ a\text{ = }((2\pi)^2)/(1) \\ a\text{ = 4}\pi^2 \\ a=4(3.142)^2 \\ a\text{ = }39.49m/s^2 \end{gathered}`