Question

5) Each table represents a proportional relationship. (From Unit 2 Lesson 2) a) Fill in the missing parts of the table. b) Draw a circle around the constant of proportionality. a х у a b т n 2 10 12 3 15 20 10 3 735 5 10 18 1 1 1

Answer 1

Given:

The table represents a proportional relationship.

a) To find the missing values of table,

For first table,

`\begin{gathered} (10)/(2)=(15)/(x) \\ 10x=15*2 \\ 10x=30 \\ x=(30)/(10)=3 \\ (15)/(3)=(y)/(7) \\ 15*7=3y \\ 3y=105 \\ y=(105)/(3)=35 \\ (35)/(7)=(y)/(1) \\ 35=7y \\ y=(35)/(7)=5 \end{gathered}`

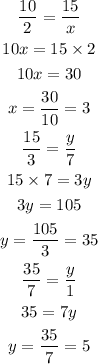
For second table,

`(3)/(12)=(b)/(20)=(10)/(a)=(b)/(1)`

`\begin{gathered} (3)/(12)=(b)/(20) \\ 3*20=12y \\ b=(60)/(12)=5 \\ (5)/(20)=(10)/(a) \\ 5a=10*20 \\ a=(200)/(5)=40 \\ (10)/(40)=(b)/(1) \\ 40b=10 \\ b=(10)/(40)=(1)/(4) \end{gathered}`

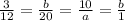
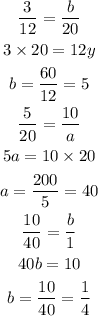
For third table,

`\begin{gathered} (3)/(5)=(n)/(10)=(18)/(m)=(n)/(1) \\ (3)/(5)=(n)/(10) \\ 30=5n \\ n=(30)/(5)=6 \\ (3)/(5)=(18)/(m) \\ 3m=90 \\ m=30 \\ (3)/(5)=(n)/(1) \\ 5n=3 \\ n=(3)/(5) \end{gathered}`

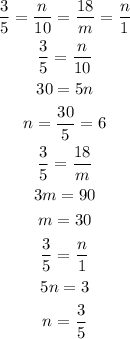
b) To draw the circle around the constant of proportionality.

For first table the constant of proportionality is 5.

For second table the constant of proportionality is 1/4.

For third table the constant of proportionality is 3/5 .