2nd Question)
1) Considering that this is a line segment R(5,8) and P(3,6). Let's find out the distance between those points using the distance formula, derived from the Pythagorean Theorem:
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)} \\ d=\sqrt[]{(3-5)^2+(6-8)^2} \\ d=2\sqrt[]{2}\approx2.82 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/v1pend61u3avzpvow48rcj98gjdzpzvxxk.png)
2) Let's now find the slope between those points, making use of the slope:
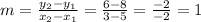
The next step is to fill in the table, so:
m: 1
Parallel slopes are identical so we can state:
║m = 1
Perpendicula