Question

a rectangle is drawn so the width is 71 inches longer than the height if the rectangles diagonal measurement is 85 inches find the heightround to 1 decimal place______inches

Answer 1

Let's first conceptualize the given details by drawing a rectangle with the given details being reflected.

Where,

x = Height of the rectangle

x + 71 = The ratio of the width of the rectangle with respect to the height.

Cutting the rectangle in half along the diagonal line makes a right triangle,

Thus, we can use the Pythagorean Theorem to be able to determine the height of the rectangle. We get,

`\text{ a}^2+b^2=c^2\text{ }\rightarrow(x+71)^2+(x)^2=(81)^2_{}`
`\text{ x}^2+142x+5041+x^2\text{ = 6561}`
`\text{ 2x}^2\text{ + 142x + 5041 - 6561 = 0}`
`((1)/(2))\text{ (2x}^2\text{ + 142x - }1520)\text{ = 0}`
`\text{ x}^2\text{ + 71x - 760 = 0}`
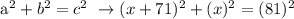
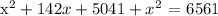
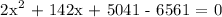
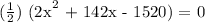
`\text{ (x +}\frac{71+\sqrt[]{8081}}{2})(x\text{ + }\frac{71\text{ - }\sqrt[]{8081}}{2})=\text{ 0}`

There are two possible height of the rectangle,

`x_1\text{ = }\frac{-71-\sqrt[]{8081}}{2}\text{ = -80.45 in.}`
`\text{ x}_2\text{ = }\frac{-71\text{ + }\sqrt[]{8081}}{2\text{ }}=9.45\text{ in.}`

9.45 = 9.5 in. is the most probable height of the rectangle because a dimension must never be negative, thus, let's adopt 9.5 in. as the height.

The width must be = x + 71 = 9.5 + 71 = 80.5 in.