Answer:
D An isosceles triangle
Step-by-step explanation:
Given that the angles of a triangle are represented by;
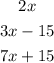
Recall that the sum of angles in a triangles is equal to 180 degrees.
Summing up the given angles we have;
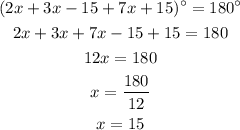
We have calculated the value of x.
We now need to calculate the value of each angle;
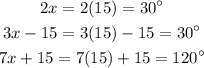
Therefore, the angles of the triangle are;

From the derived angles, we can notice that the triangle has two equal angles.
So it is an Isosceles triangle.