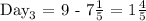Translating for numbers, we have:

This way, we can make what follows:
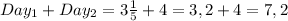
Calculating now the amount is needed to complete the 9 miles:

--------------------------------------------------------------------------------------------------------
And from here, the solution with the fractions.
We can start with the sum of what Shelly has biked in the first two days:
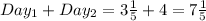
This is the amount of mile she has already biked. But we know she needs to complete all the 9 miles in the third day. So, the difference from 9 and the amount she already did is the amount she needs to bike in the third day.