Question

Determine whether the dilation from A to B is an enlargement or a reduction. Then find the scale factor of the dilation.

Answer 1

From the figure we notice that the figure B is smaller than figure A, hence the dilation is a reduction.

Now, to find the dilation factor we notice that the right side of figure A has length 6; the same side for figure B has length 2; then we need to find a factor that fullfils:

`6k=2`

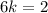
solving for k we have that:

`\begin{gathered} 6k=2 \\ k=(2)/(6) \\ k=(1)/(3) \end{gathered}`

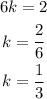
Therefore the scale factor of the dilation is 1/3