Question

For a given geometric sequence, the common ratio, r, is equal to -3, and the 11th term, a₁, is equal to 11. Find the value of the 13thterm, a13. If applicable, write your answer as a fraction.a13

Answer 1

Given:

Common ratio=-3

11th term=11

To determine the 13th term, we first note the geometric sequence formula:

`a_n=ar^(n-1)`

where:

a=1st term

n=nth term

Since the 11th term is 11, we can solve the first term by following the process as shown below:

`\begin{gathered} a_(n)=ar^(n-1) \\ a_(11)=a(-3)^(11-1) \\ 11=a(-3)^(10) \\ Simplify \\ a=(11)/(59049) \end{gathered}`

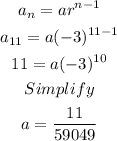
Next, we plug in a=11/59049 when n=13:

`\begin{gathered} a_(n)=ar^(n-1) \\ a_(13)=((11)/(59049))(-3)^(13-1) \\ Calculate \\ a_(13)=99 \end{gathered}`

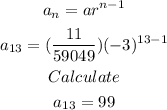
Therefore, the answer is: 99