Question

I need help in math can you please help me please

Answer 1

Trigonometric Equations

Solve:

`9\tan ^3x=3\tan x`

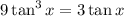
In the interval [0,2pi)

We have to find all the values of x that make equality stand. First, divide by 3:

`3\tan ^3x=\tan x`

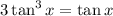
Subtract tan x

`3\tan ^3x-\tan x=0`

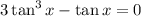
Factor tan x out:

`\tan x(3\tan ^2x-1)=0`

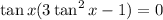
One solution comes immediately:

tan x = 0

There are two angles whose tangent is 0:

`x=0\text{ , x=}\pi`

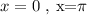
The other solutions come when equating:

`3\tan ^2x-1=0`

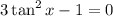
Adding 1, and dividing by 3:

`\tan ^2x=(1)/(3)`

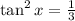
Taking the square root:

`\tan x=\sqrt[\square]{(1)/(3)}=\pm\frac{\sqrt[]{3}}{3}`

The positive answer gives us two solutions:

`\tan x=\frac{\sqrt[]{3}}{3}`

x=pi/6 and x=7pi/6

The negative answer also gives us two solutions:

`\tan x=-\frac{\sqrt[]{3}}{3}`

x=5pi/6, 11pi/6

Summarizing the solutions are:

{