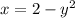When you have a function written in explicit form with two variables(let's call them 'x' and 'y'), it is written as a combination of 'x' and 'y' equal to some constant.
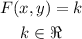
To "solve for x in terms of y", is the same as rewritting this function as an equality in the following form:
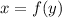
Let's try an example to show how this works.
Given the following function:
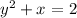
Now, solving for x in terms of y, is the same as rewriting x as a function of y.