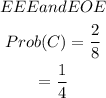Question

Thank you for viewing my question I seem to be stuck on this and need help thank you

Answer 1

`\begin{gathered} A=(1)/(4) \\ B=(1)/(2) \\ C=(1)/(4) \end{gathered}`

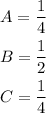
Step-by-step explanation

From the given data;

Event A; Alternating even and odd numbers means;

EOE and OEO

Number of favourable outcome is 2 while number of possible outcome is 8

Hence, the probability of Event A IS;

`\begin{gathered} Prob(A)=(2)/(8) \\ =(1)/(4) \end{gathered}`

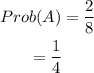
In Event B; More even numbers than odd means having;

EEE,OEE,EEO and EOE

`\begin{gathered} EEE,OEE,EEOandEOE \\ Prob(B)=(4)/(8) \\ =(1)/(2) \end{gathered}`

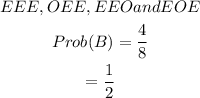
For Event C; an even number on both the first and the last rolls;

EEE and EOE

`\begin{gathered} EEEandEOE \\ Prob(C)=(2)/(8) \\ =(1)/(4) \end{gathered}`