Question

How many solutions exist for the equation cos 2θ − sin θ = 0 on the interval [0, 360°)?

Answer 1

I got it correct, by graphing on desmos

Explanation:

Look at picture

Answer 2

We are given the following equation

`\cos 2\theta-\sin \theta=0`

Let us solve the above trigonometric equation.

Using the double angle identity,

`\cos 2\theta=1-2\sin ^2\theta`

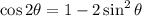
So, the equation becomes

`\begin{gathered} \cos 2\theta-\sin \theta=0 \\ 1-2\sin ^2\theta-\sin \theta=0 \end{gathered}`

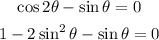
Now, let us solve the equation by substitution

Let sinθ = u

`\begin{gathered} 1-2\sin ^2\theta-\sin \theta=0 \\ 1-2u^2-u=0 \\ -2u^2-u+1=0 \end{gathered}`

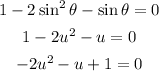
Let us solve the above equation using the quadratic formula

`u=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

The coefficients are

a = -2

b = -1

c = 1

`\begin{gathered} u=\frac{-(-1)\pm\sqrt[]{(-1)^2-4(-2)(1)}}{2(-2)} \\ u=\frac{1\pm\sqrt[]{1+8}}{-4} \\ u=\frac{1\pm\sqrt[]{9}}{-4} \\ u=(1\pm3)/(-4) \\ u=(1-3)/(-4),\; \; u=(1+3)/(-4) \\ u=(-2)/(-4),\; \; u=(4)/(-4) \\ u=(1)/(2),\; \; u=-1 \end{gathered}`

So, the two possible values are u = 1/2 and u = -1

Substitute them back into sinθ = u

`\begin{gathered} \sin \theta=(1)/(2),\; \; \sin \theta=-1 \\ \theta=\sin ^(-1)((1)/(2)),\; \; \theta=\sin ^(-1)(-1) \\ \theta=(\pi)/(6)\; and\; (5\pi)/(6),\; \; \theta=(3\pi)/(2)\; \\ \theta=30\degree\; and\; \; 150\degree,\; \; \theta=270\degree \end{gathered}`

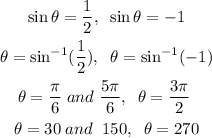
Therefore, the two solutions of the given equation are θ = 30°, θ = 150°, θ = 270° on the interval [0, 360°)