Given:
Mean = 22.90
Standard Deviation = 4.90
Find the cutoff price so that 45% of all cases are priced below that amount.
To solve this problem, the first thing we need to do is to find the z-score for 45% or 0.45.
The z-score for 0.45 is -0.126.
Now, to find the cutoff price or the "score", we will use the following equation

Where:
z = z-score
x = score
μ = mean
σ = standard deviation
We are looking for the "x"
Derive the formula and substitute the given data.

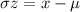
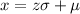
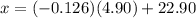
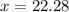
We got a value of 22.28 for our score, therefore, the cutoff price must be $22.28.