Question

GRE verbal reasoning scores has an unknowndistribution with a mean of 150.1 and astandard deviation of 9.4. Using the empirical rule,what do we know about thepercentage of GRE verbal reasoning scoresbetween 131.3 and 168.9?

Answer 1

Empirically we can see the σ ranges of a Gaussian distribution in the following figure

From exercise we know that:

`\begin{gathered} \bar{x}\bar{}=150.1 \\ \sigma=9.4 \end{gathered}`

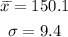
We will calculate how many sigmas the given range is to know what the percentage of scores :

`\begin{gathered} x=\bar{x}-A\sigma \\ x=131.3 \\ 131.3=150.1-A(9.4) \\ 150.1-131.3=9.4A \\ A=(18.8)/(9.4) \\ A=2 \\ \end{gathered}`

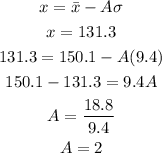
The score 131.3 is 2 sigmas from the mean

`\begin{gathered} x=\bar{x}+A\sigma \\ x=168.9 \\ 168.9=150.1-A(9.4) \\ 168.9-150.1=9.4A \\ A=(18.8)/(9.4) \\ A=2 \end{gathered}`

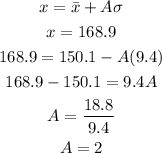
The score 168.9 is 2 sigmas from the mean

The range of reasoning scores between 131.3 and 168.9 is ±2σ which corresponds to 95.5% (see initial graph)