Question

Ms. Friedman and Mrs. Elliot both teachsixth grade math. They share a storagecloset. What is the total area of both roomsand the storage closet?

Answer 1

The two classrooms are identical in length and width. On the other hand, the dimensions of the storage closet are

`(40-34)*(36-30)=6*6`

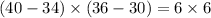
The shape of both classrooms and the storage closet is rectangular; therefore, their areas are

`\begin{gathered} A_{\text{rectangle}}=l\cdot w\to length\cdot width_{} \\ \Rightarrow A_{\text{Friedman}}=40\cdot36 \\ _{}A_{\text{Elliot}}=40\cdot36 \\ A_(storage)=6\cdot6 \\ \end{gathered}`

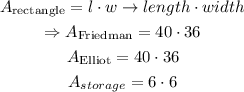
Simplifying,

`\begin{gathered} \Rightarrow A_{\text{storage}}=36ft^2 \\ \Rightarrow A_{\text{Friedman}}=A_{\text{Elliot}}=1440ft^2 \end{gathered}`

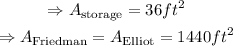
Finally, the total area of the compound is

`\begin{gathered} A_{\text{total}}=A_{\text{Friedman}}+A_{\text{Elliot}}-A_{\text{storage}} \\ \Rightarrow A_{\text{total}}=2\cdot1440-36=2844 \end{gathered}`

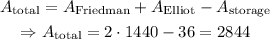
Thus, the total area of the two classrooms plus the closet is 2844ft^2

Then,