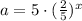Find the formula for an exponential equation that passes through the points, (0,5) and (1,2). The exponential equation should be of the form y = ab^x

Question

asked Dec 27, 2023 167k views

2 Answers

Steve Peschka · Answer 1 · 2023-12-31T14:17:36+0000

Answer:

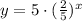
$y=5\cdot((2)/(5))^x$

Step-by-step explanation:

The exponential equation has the form

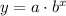
$y=a\cdot b^x$

Since it passes through the point (0, 5). Let's replace (x, y) by (0, 5) to find the value of a

$\begin{gathered} 5=a\cdot b^0 \\ 5=a\cdot1 \\ 5=a \end{gathered}$

Then, the equation is

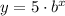
$y=5\cdot b^x$

To find the value of b, we will use the point (1, 2), so replacing x = 1 and y = 2, we get:

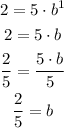
$\begin{gathered} 2=5\cdot b^1 \\ 2=5\cdot b \\ (2)/(5)=(5\cdot b)/(5) \\ (2)/(5)=b \end{gathered}$

Then, the exponential equation is:

$a=5\cdot((2)/(5))^x$