1 Answer

Suppressingfire · Answer 1 · 2023-08-20T22:41:00+0000

Given the radical equation:

$q-6=\sqrt[]{27-2q}$

Squaring both sides to eliminate the root.

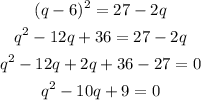
$\begin{gathered} (q-6)^2=27-2q \\ q^2-12q+36=27-2q \\ q^2-12q+2q+36-27=0 \\ q^2-10q+9=0 \end{gathered}$

Factor the equation to find the roots:

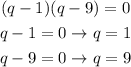
$\begin{gathered} (q-1)(q-9)=0 \\ q-1=0\rightarrow q=1 \\ q-9=0\rightarrow q=9 \end{gathered}$

we will check ( q = 1 and q = 9 ) by substitution into the given equation:

When q = 1

$\begin{gathered} q-6=1-6=-5 \\ \sqrt[]{27-2q}=\sqrt[]{27-2}=\sqrt[]{25}=5 \end{gathered}$

So, ( q = 1 ) is an extraneous solution.

When q = 9

$\begin{gathered} q-6=9-6=3 \\ \sqrt[]{27-2q}=\sqrt[]{27-18}=\sqrt[]{9}=3 \end{gathered}$

So, ( q = 9 ) is the solution of the given equation.

So, the answer will be:

The extraneous solution to the radical equation is 1

Please log in or register to add a comment.