We have the next variables
x = speed of the boat in still water
y = speed of the current
(x-y) = Upstream speed
(x+y) = downstream speed
So we have the next equations for the distance
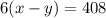
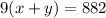
We simplify each equation
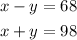
we sum both equations
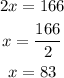
Then we calculate the y
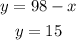
x = speed of the boat in still water=83 km/hr
y = speed of the current 15 km/hr